Fuvest 2018 Uma caminhonete, de massa 2.000 kg, bateu na traseira de um sedã

Uma caminhonete, de massa 2.000 kg, bateu na traseira de um sedã, de massa 1.000 kg, que estava parado no semáforo, em uma rua horizontal. Após o impacto, os dois veículos deslizaram como um único bloco. Para a perícia, o motorista da caminhonete alegou que estava a menos de 20 km/h quando o acidente ocorreu. A perícia constatou, analisando as marcas de frenagem, que a caminhonete arrastou o sedã, em linha reta, por uma distância de 10 m. Com este dado e estimando que o coeficiente de atrito cinético entre os pneus dos veículos e o asfalto, no local do acidente, era 0,5, a perícia concluiu que a velocidade real da caminhonete, em km/h, no momento da colisão era, aproximadamente,

(A) 10.

(B) 15.

(C) 36.

(D) 48.

(E) 54.

Note e adote: Aceleração da gravidade: 10 m/s2. Desconsidere a massa dos motoristas e a resistência do ar.

Tags – Física, Força de Atrito, Conservação da quantidade de movimento, colisão inelástica, forças dissipativas.

Resolução

Para facilitar a resolução dividiremos o problema em duas partes: i) calcular a velocidade dos corpos pós choque para que eles tenham percorrido 10 m e ii) calcular a velocidade da caminhonete para que eles tenham saído com essa velocidade.

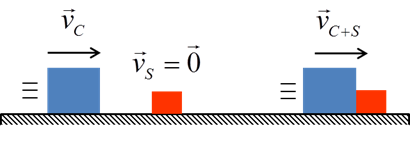
Conforme o enunciado, após a colisão os veículos deslizarão como um único bloco com velocidade v_C+S. Desenhando o diagrama de corpo livre desse bloco:

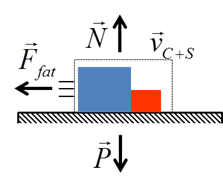
A resultante de forças do corpo na vertical será nula – N=P=(2000+1000)x10 -, no entanto na horizontal ele possuirá uma resultante F_fat contrária a direção do seu deslocamento gerada pelo atrito entre os veículos e o solo. Como os veículos após o choque permanecem em movimento, o atrito será do tipo cinético e portanto:

F_fat=μ_cxN=0,5x(2000+1000)kgx10m/s²= 15000 N

Como o atrito é o único responsável por dissipar energia durante esse deslocamento, temos que a variação da energia mecânica será igual ao trabalho realizado pela força de atrito:

τ_fat = ΔE_M = ΔE_C = M x (v²_f(C+S)- v²_i(C+S))/2

15000N x 10m=[3000kg x (0- v²_i(C+S)) m²/s²]/2

v²_i(C+S)=100

v_i(C+S) = 10 m/s

Como não há forças externas durante a colisão podemos aplicar conservação da quantidade de movimento:

Q_i=Q_f → M x v_(C+S)= m_C x v_C + m_S x v_S = m_C x v_C

3000 x 10 = 2000 x v_c

v_c = 15 m/s

Sabendo que 1 m/s = 3,6 km/h:

v_c = 15 x 3,6 km/h = 54 km/h

Alternativa E.