Fuvest 2018 Sejam  Df e Dg os maiores subconjuntos de R nos quais estão definidas

Sejam  D_f e D_g os maiores subconjuntos de R nos quais estão definidas, respectivamente, as funções reais

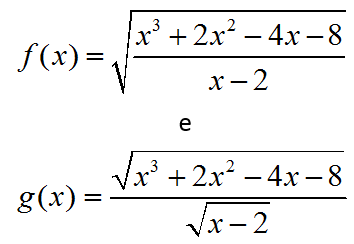
Considere, ainda, I_f e I_g   as imagens de f e de g, respectivamente.

Nessas condições,

1.  D_f =  D_g e I_f = I_g
2. Tanto D_f e  D_g  quanto I_f e I_g   diferem em apenas um ponto.
3. D_f e  D_g diferem em apenas um ponto,  I_f e I_g e  diferem em mais de um ponto.
4. D_f e  D_g diferem em mais de um ponto,   I_f e I_g  diferem em apenas um ponto.
5. Tanto D_f e  D_g  quanto I_f e I_g   diferem em mais de um ponto.

 Tags – Matemática, determinação de domínios, determinação do conjunto imagem, estudo de sinais de uma função, esboço de gráficos, função modular.

Resolução

Divisões por zero e raízes negativas não são definidos nos reais, logo a função f não é definida para x-2=0 → x=2 e para valores em que o radicando é negativo. Observe que 2 é uma das raízes do numerador, portanto podemos simplificar o radicando :

 

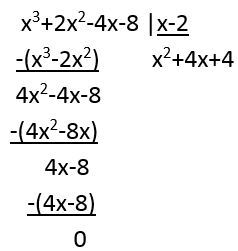
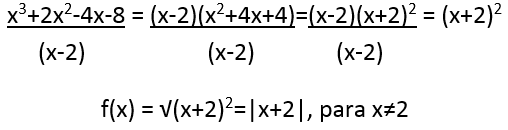
f(x) = √(x+2)²=|x+2|, para x≠2

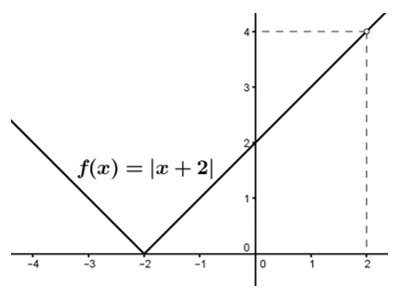
Como (x+2)² é positivo para todo valor de x real, não teremos problema com radicando negativo, logo a função f  é definida para todo valor de x ϵ R-{2} (D_f = R-{2} e I_f = R₊^*}.

Para a função g, ambas as raízes devem ser determinadas, logo x³+2x²-4x-8 e x-2 devem ser não negativas. Como visto anteriormente a radicando do numerador pode ser fatorado em (x-2)(x+2)(x+2), estudando o sinal dessas funções temos que:

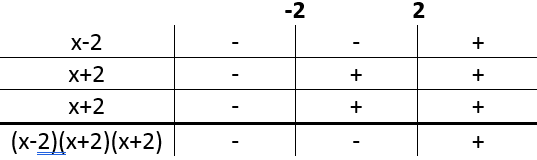
Observe que o sinal de cada linha é dado pelo estudo de sinal das retas e o sinal da última linha é dado pelo produto entre os sinais da coluna. Portanto, a função g só está definida para x > 2, já que em x = 2 caímos em uma divisão por zero e para x<2 teremos radicandos negativos. No domínio em que o numerador e o denominador de g estão definidos podemos simplifica-lo para g(x) =|x+2|, assim I_g=]4,∞[.

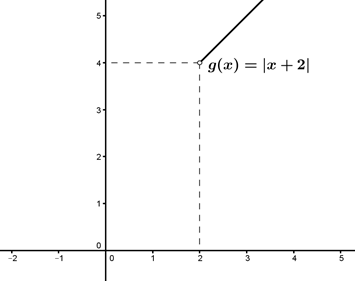
Portanto, a alternativa correta é a E, pois tanto D_f e D_g quanto I_f e I_g diferem em mais de um ponto.

letra E