Prolongando se os lados de um octógono convexo ABCDEFGH, obtém se um polígono estrelado, conforme a figura.
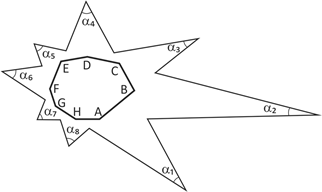
A soma α1 + … + α8 vale:
(A) 180°.
(B) 360°.
(C) 540°.
(D) 720°.
(E) 900°.
Tags – Matemática, ângulos, soma de ângulos internos, polígonos convexos e não convexos.
Resolução
Tracemos os prolongamentos dos lados do octógono:
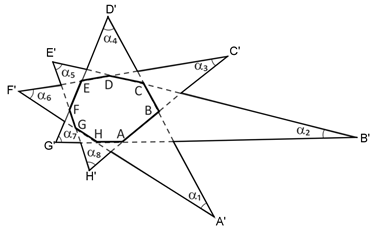
Observe os quadriláteros convexos E’CA’G, D’BH’F’, C’AG’E e B’HF’D:
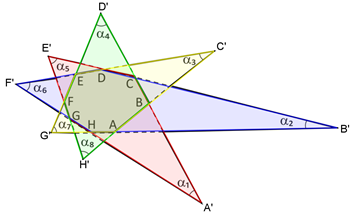
A soma dos ângulos internos de cada um desses quadriláteros é 360º, logo:
α5 + α1 + g + c = 360º
α4 + α8 + f + b = 360º
α3 + α7 + e + a = 360º
α2 + α6 + h +d = 360º
Somando as 4 equações temos que:
α1 + α2 + α3 + α4 + α5 + α6 + α7 + α8 + a + b + c + d + e + f + g + h = 1440º
Sabendo que a soma dos ângulos internos de um polígono convexo de n lados é calculada pela expressão:
Sn = (n-2) x 180º
Temos que a soma dos ângulos internos do octógono (a + b + c + d + e + f + g + h) é igual a (8-2) x 180º = 1080º. Portanto:
α1 + α2 + α3 + α4 + α5 + α6 + α7 + α8 = 1440 º – 1080º = 360º
Alternativa B.
