O quadrilátero da figura está inscrito em uma circunferência de raio 1. A diagonal desenhada é um diâmetro dessa circunferência.
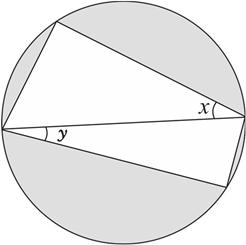
Sendo e as medidas dos ângulos indicados na figura, a área da região cinza, em função de e , é:
(A) π + sen(2x) + sex(2y)
(B) π – sen(2x) – sex(2y)
(C) π – cos(2x) + cos(2y)
(D) π – (cos(2x) + cos(2y))/2
(E) π – (sen(2x) + sen(2y))/2
Tags – Matemática, trigonometria
Resolução
Ângulo inscrito relativo a uma circunferência é aquele que tem o vértice na circunferência:
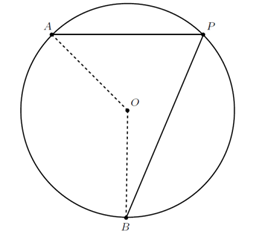
Assim, ∠APB é o ângulo inscrito e ∠AOB é o ângulo central que é igual à medida do arco determinado na circunferência pelos pontos A e B que não contém P.
O teorema do ângulo inscrito nos diz que o ângulo inscrito é metade do ângulo central correspondente, assim ∠APB=(∠AOB)/2.
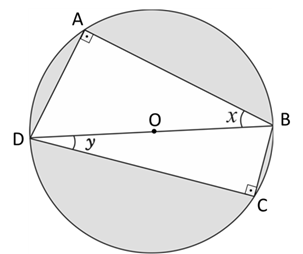
Desse modo, em nossa questão o ângulo ∠DOB = 180º é o ângulo central correspondente aos ângulos ∠DAB e ∠DCB, logo ∠DAB = ∠DCB 90º.
Esse fato nos é interessante, pois podemos calcular a área da região cinza subtraindo da área total a área dos triângulos retângulos ΔABD e ΔCDB.
Como o raio da circunferência é igual a 1, sua área é dada por AC=πR2= π.12 = π e o seu diâmetro DB vale 2. Pelas definições de seno e cosseno no triângulo retângulo temos que:
sen(x) = (cateto oposto a x)/(hipotenusa) = (AD)/(DB) → AD = (DB)sen(x)
cos(x) = (cateto adjacente a x)/(hipotenusa) = (AB)/(DB) → AB = (DB)sen(x)
Assim,
os lados de ΔABD são 2sen(x) e 2cos(x) e
os lados de ΔCDB são 2sen(y) e 2cos(y),
portanto suas áreas são 2sen(x)cos(x) e 2sen(y)cos(y), respectivamente.
Logo a área da região cinza é
π – 2sen(x)cos(x) – 2sen(y)cos(y).
A fórmula para o seno da soma de arcos é:
sen(a+b) = sen(a)cos(b) + sen(b)cos(a)
Assim, quando a=b a fórmula se reduz a:
sen(2a) = 2sen(a)cos(a)
Portanto, substituindo 2sen(x)cos(x) e 2sen(y)cos(y) na área encontrada por sen(2x) e sen(2y), respectivamente, temos que a resposta final é
π – sen(2x) – sen(2y).
alternativa B.
