Fuvest 2018 O projeto para um balanço de corda única de um parque de diversões exige

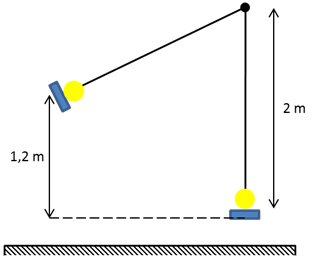
O projeto para um balanço de corda única de um parque de diversões exige que a corda do brinquedo tenha um comprimento de 2,0 m. O projetista tem que escolher a corda adequada para o balanço, a partir de cinco ofertas disponíveis no mercado, cada uma delas com distintas tensões de ruptura. A tabela apresenta essas opções.

Corda	I	II	III	IV	V
Tensão de ruptura (N)	4.200	7.500	12.400	20.000	29.000

 

Ele tem também que incluir no projeto uma margem de segurança; esse fator de segurança é tipicamente 7, ou seja, o balanço deverá suportar cargas sete vezes a tensão no ponto mais baixo da trajetória. Admitindo que uma pessoa de 60 kg, ao se balançar, parta do repouso, de uma altura de 1,2 m em relação à posição de equilíbrio do balanço, as cordas que poderiam ser adequadas para o projeto são

1. I, II, III, IV e
2. II, III, IV e V,
3. III, IV e V,
4. IV e V,
5. V,

Note e adote: Aceleração da gravidade: 10 m/s2. Desconsidere qualquer tipo de atrito ou resistência ao movimento e ignore a massa do balanço e as dimensões da pessoa. As cordas são inextensíveis.

  Tags – Física, aceleração centrípeta, conservação da energia mecânica, tensão em corda, movimento circular.

Resolução

Primeiramente vamos determinar a velocidade com que o balanço chega ao seu ponto mais baixo (posição de equilíbrio). Para tal podemos utilizar a conservação de energia mecânica que ocorre do ponto em que a pessoa está a 1,2 m do ponto mais baixo até a posição de equilíbrio já que nesse trajeto o corpo está apenas sob a ação de forças conservativas:

E_Mi=E_Mf

E_pi + E_ci = E_pf + E_cf → E_pi = E_cf

mgh=mv²/2 → 10 m/s² x 1,2 m = v²/2

v² = 24 m²/s²

Observe que o movimento realizado pelo balanço é circular, portanto podemos igualar a resultante de forças no ponto mais baixo à força centrípeta. Construindo o diagrama de corpo livre:

 

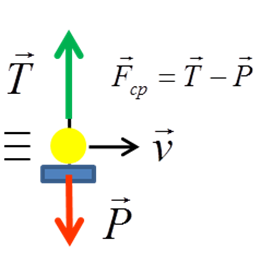
T – P = F_cp = mv²/R

T = mv²/2 + mg = 60 x 24/2 + 60 x 10 = 1320 N

Portanto a tensão no ponto mais baixo é de 1320 N, como precisamos de uma margem de segurança de 7 vezes essa tensão, a corda deve aguentar no mínimo T_s=7 x 1320 = 9240 N, portanto as cordas III, IV e V são adequadas.

Alternativa C.