Fuvest 2018 Em uma urna, há bolas amarelas, brancas e vermelhas. Sabe-se que

Em uma urna, há bolas amarelas, brancas e vermelhas. Sabe-se que:

1. A probabilidade de retirar uma bola vermelha dessa urna é o dobro da probabilidade de retirar uma bola
2. Se forem retiradas 4 bolas amarelas dessa urna, a probabilidade de retirar uma bola vermelha passa a ser 1/2.

• Se forem retiradas 12 bolas vermelhas dessa urna, a probabilidade de retirar uma bola branca passa a ser 1/2.

A quantidade de bolas brancas na urna é

(A) 8.

(B) 10.

(C) 12.

(D) 14.

(E) 16.

 Tags – Matemática, probabilidade, sistema de equações, equacionamento de problemas.

Resolução

Seja A, B e V, respectivamente, a quantidade de bolinhas da urna nas cores amarela, vermelha e verde. Do enunciado, temos que:

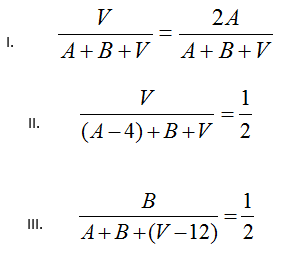
Como a quantidade total de bolinhas é diferente zero, de I. temos que . Substituindo em II. e III.:

 

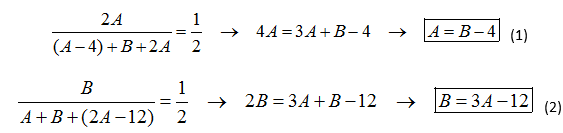
Substituindo (2) em (1), chegamos a alternativa C:

A = (3A – 12) – 4

2A = 16

A = 8

V = 2A = 16

B = A + 4 = 12 

letra C