Doze pontos são assinalados sobre quatro segmentos de reta de forma que três pontos sobre três segmentos distintos nunca são colineares, como na figura.
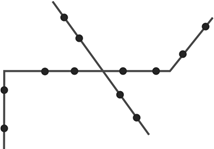
O número de triângulos distintos que podem ser desenhados com os vértices nos pontos assinalados é
(A) 200.
(B) 204.
(C) 208.
(D) 212.
(E) 220.
Tags – Matemática, combinatória, definição de triângulo, identificação de casos não adequados.
Resolução
Para formarmos um triângulo basta escolhermos 3 pontos não colineares. Desse modo, todas as escolhas de pontos na figura formam triângulos menos aquelas em que os pontos são colineares. Como há um total de 12 pontos, podemos escolher 3 pontos quaisquer – não importando a ordem, pois queremos triângulos distintos – pela combinação C12,3, sabendo que a combinação de Cn,p é dada por:
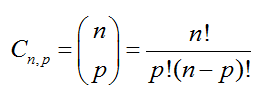
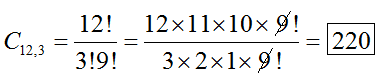
C12,3 = 12! ÷ (3! 9!) = 220
No entanto, como só queremos as escolhas que formam triângulos, devemos calcular de quantos modos podemos escolher 3 pontos colineares na figura e subtrair esse valor do total de possibilidades de escolher 3 pontos quaisquer.
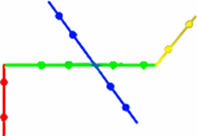
Note que na figura só podemos escolher três pontos colineares na reta verde ou na reta azul. Em cada uma delas o total de possibilidades de realizar tal escolha é:
C4,3 = 4! ÷ (1!3!) = 4
Portanto, o número de triângulos distintos que podem ser desenhados com os vértices nos pontos assinalados é:
220 – 2×4 = 212
Alternativa D.
