Fuvest 2018 Dois atletas correm com velocidades constantes em uma pista retilínea

Dois atletas correm com velocidades constantes em uma pista retilínea, partindo simultaneamente de extremos opostos, A e B. Um dos corredores parte de A, chega a B e volta para A. O outro corredor parte de B, chega a A e volta para B. Os corredores cruzam se duas vezes, a primeira vez a 800 metros de A e a segunda vez a 500 metros de B. O comprimento da pista, em metros, é

(A) 1.000.

(B) 1.300.

(C) 1.600.

(D) 1.900.

(E) 2.100.

Tags – Matemática, encontro de corpos.

Resolução

Chamemos de V_A a velocidade do corredor que sai de A e V_B a velocidade do corredor que sai de B. As possíveis configurações dos encontros são:

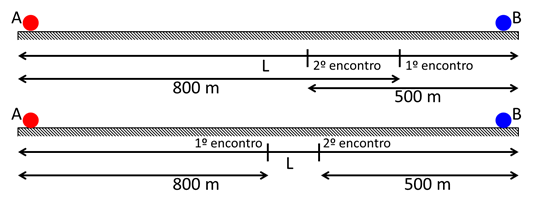
Em que L é o comprimento total da pista e no primeiro caso L < 800 m + 500 m, e no segundo caso L > 1300 m. Como ambos partem simultaneamente de suas posições iniciais, o tempo de chegada até o 1º encontro é o mesmo, como as velocidades são constantes, esse tempo é dado por Δt = Δs/v, logo, para o primeiro encontro:

Δt_A1 = Δt_B1 → 800/V_A = (L-800)/V_B  → V_B/V_A = (L-800)/800

Para o segundo encontro, o corredor A pode ter encontrado o corredor B quando o B estava indo ainda para o ponto A ou quando o corredor B estava voltando do ponto A, no primeiro caso:

Δt_A2 = Δt_B2 → (L+500)/V_A = 500/V_B  → V_B/V_A = 500/(L+500)

Igualando a equação anterior:

V_B/V_A = (L-800)/800 = 500/(L+500) → L² – 300L – 400.000 = 400.000 → L² – 300L – 800.000 = 0

L₁ ≅ 1.057 m (não está entre as alternativas)  L₂ ≅ 756 m (absurdo L > 800m)

Logo o encontro ocorreu enquanto o corredor B voltava do ponto A:

Δt_A2 = Δt_B2 → (L+500)/V_A = (L+L-500)/V_B  → V_B/V_A = (2L-500)/(L+500)

(L-800)/800 = (2L-500)/(L+500) → L² – 300L – 400.000 = 1.600L – 400.000 → L² – 1.900L = 0

L₁ = 0 (absurdo) L₂ = 1.900 m

Alternativa D.