Dentre os candidatos que fizeram provas de matemática, português e inglês num concurso, 20 obtiveram nota mínima para aprovação nas três disciplinas. Além disso, sabe se que:
I. 14 não obtiveram nota mínima em matemática;
II. 16 não obtiveram nota mínima em português;
III. 12 não obtiveram nota mínima em inglês;
IV. 5 não obtiveram nota mínima em matemática e em português;
V. 3 não obtiveram nota mínima em matemática e em inglês;
VI. 7 não obtiveram nota mínima em português e em inglês e
VII. 2 não obtiveram nota mínima em português, matemática e inglês.
A quantidade de candidatos que participaram do concurso foi
(A) 44.
(B) 46.
(C) 47.
(D) 48.
(E) 49.
Tags – Matemática, diagrama de Venn, conjuntos, teoria dos conjuntos
Resolução
Diagrama de Venn é um método visual criado por John Venn para representar a relação entre conjuntos. O método consiste em representarmos os conjuntos por figuras (em geral círculos) e as relações de pertencimento e intersecção pela posição dessas. Seja o círculo azul a representação do conjunto A={0,2,4,6,8,10} e o círculo vermelho a representação do conjunto B={0,3,6,9}, o conjunto resultante da intersecção entre A e B (A∩B={0,6}) é representado pela região lilás entre os dois círculos:
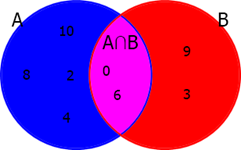
E ambos os conjuntos pertencem ao conjunto dos naturais representado pelo retângulo verde:
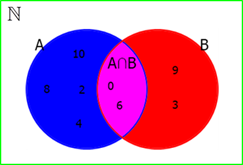
Com essas noções em mente podemos resolver o problema utilizando o diagrama de Venn para nos auxiliar:
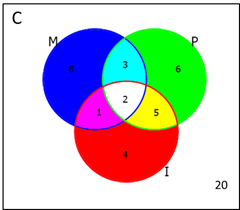
M é o conjunto dos que não obtiveram nota mínima em matemática, P dos que não obtiveram nota mínima em português, I dos que não obtiveram nota mínima em inglês e C o conjunto dos candidatos que participaram do concurso.
Começamos preenchendo o diagrama do centro com a quantidade de elementos do conjunto M∩P∩I , em seguida as regiões de intersecção M∩P, M∩I e P∩I, lembrando que M∩P∩I está contido nesses conjuntos portanto se o total de elementos de M∩P é 5, como já indicamos que há 2 elementos na região branca, basta indicarmos os 3 restantes na região ciano (a região ciano representa o conjunto M∩P-I e o conjunto M∩P é representado pela região ciano mais a região branca). Repetindo o procedimento para o restante do diagrama, completamos o diagrama acima. A quantidade total de elementos do conjunto C será dado pela soma da quantidade de elementos de cada região: 20+8+6+4+3+5+1+2=49, alternativa E.
Outra forma de resolver o problema é pela fórmula para cálculo da quantidade de elemento da união de 3 conjuntos (cardinalidade da união):
n(MUPUI)=n(M)+n(P)+n(I)-n(M∩P)-n(M∩I)-n(P∩I)+n(M∩P∩I)=14+16+12-5-3-7+2=29
n(C)= n(MUPUI)+n[C\(MUPUI)]=29+20=49
letra E
