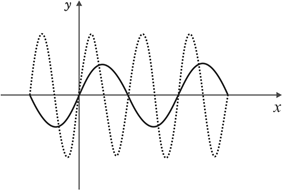
Admitindo que a linha pontilhada represente o gráfico da função e que a linha contínua represente o gráfico da função , segue que
a) 0 < α < 1 e 0 < β < 1
b) α > 1 e 0 < β < 1
c) α = 1 e β > 1
d) 0 < α < 1 e β > 1
e) 0 < α < 1 e β = 1
Tags – Matemática, funções periódicas, função seno, função cosseno, determinação de período, análise de gráfico.
Resolução
Um função é dita periódica se existe um número real T tal que f(x+T) = f(x) para todo x real, em que T é conhecido como período da função. Período fundamental é definido como o menor período de f. Se f(x) possui período T, a função g(x)=f(ax) possui período T/a. A função sen(x) e cos(x) possuem período conhecido igual a 2π.
Voltando a questão, temos que a função g possui período igual 2π/β, pelo gráfico a função g tem período igual ao dobro do período de f, portanto 2π/β = 2 x 2π → β = 0,5.
Amplitude de uma função é definida como a distância do eixo à crista (pico) ou ao vale do gráfico da função. Em uma função do tipo f(x)=Asen(x), A determina a amplitude de f. Em f(x)=sen(x) a amplitude da f é 1 e em g(x)=αsen(βx) a amplitude de g é α. Pelo gráfico, a amplitude de g é menor que a amplitude de f, portanto, α<1. Logo a alternativa correta é A.
