Um elevador sobe verticalmente com velocidade constante v0, e, em um dado instante de tempo t0, um parafuso desprende se do teto. O gráfico que melhor representa, em função do tempo t, o módulo da velocidade v desse parafuso em relação ao chão do elevador é
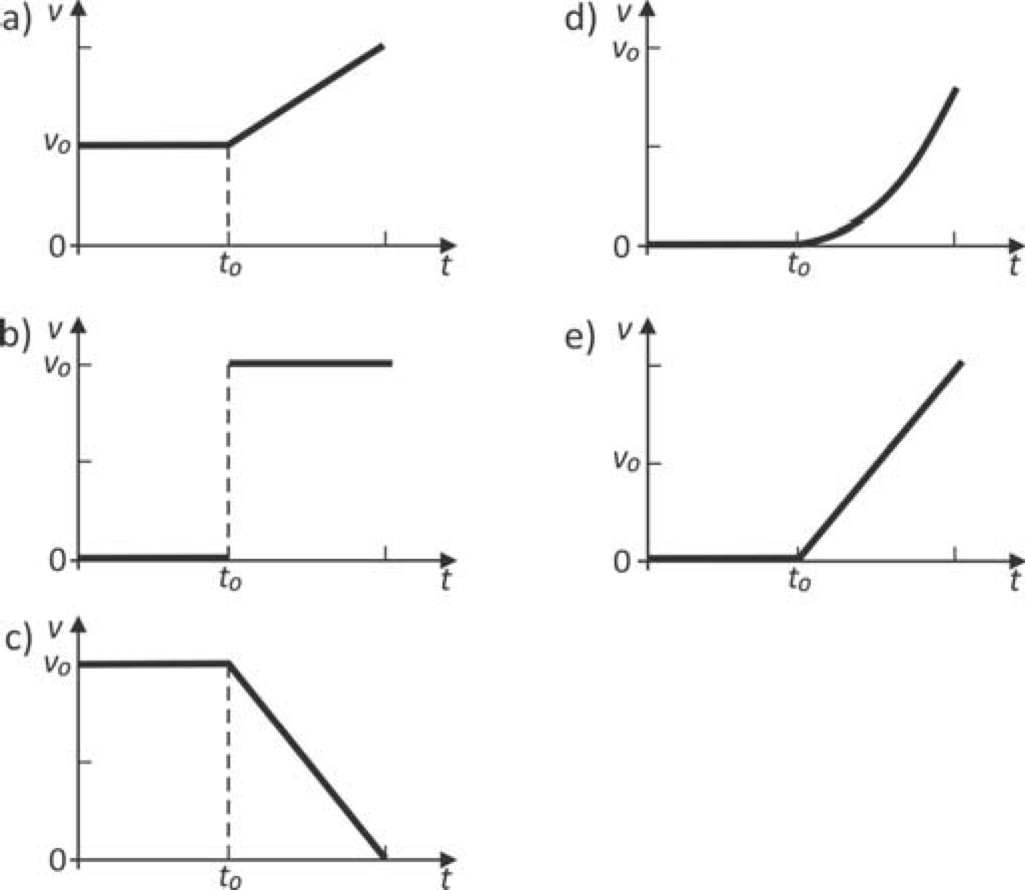
| Note e adote:
Os gráficos se referem ao movimento do parafuso antes que ele atinja o chão do elevador. |
Tags – Física, cinemática, queda livre, velocidade relativa, mudança de referencial, análise de gráfico.
Resolução
Observe a ilustração do problema abaixo:
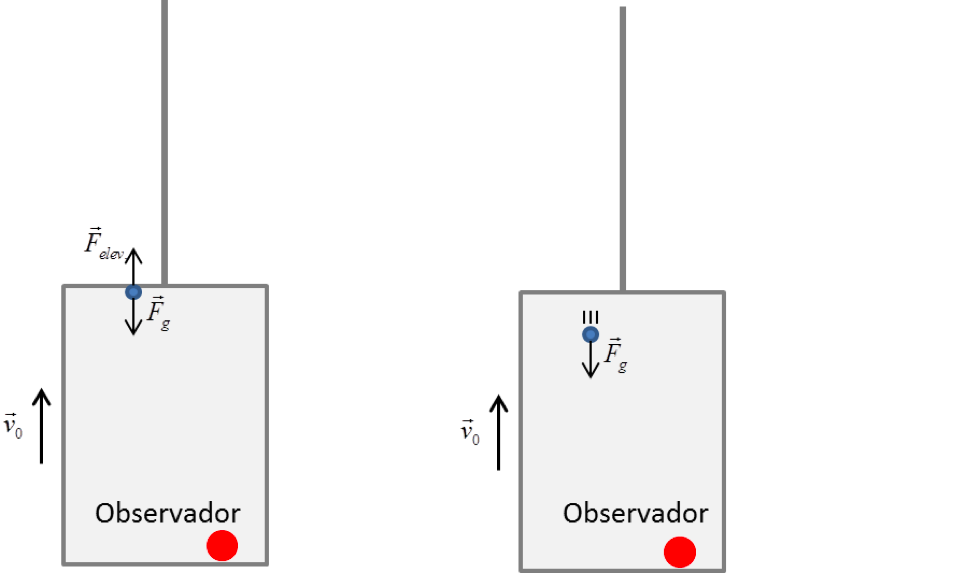
Até o instante t0 a resultante de forças sobre o parafuso é igual a zero, já que a ação da gravidade é anulada pelas forças que mantem o parafuso unido ao elevador, portanto sua velocidade permanece constante e igual a v0 (mesma velocidade do elevador). Para um observador dentro do elevador, o parafuso permanece em repouso (velocidade do parafuso em relação ao elevador). Podemos verificar essa informação pela fórmula para velocidade relativa entre dois corpos:
VAB = VA – VB (velocidade de A em relação a B)
Vparafuso-elevador = Vparafuso – Velevador = v0 – v0 = 0 m/s
A partir do instante t0, o parafuso se desprende do teto do elevador, ainda com velocidade v0, e passa a estar sujeito apenas à força da gravidade, iniciando uma queda livre. Nesse movimento sua velocidade em um instante t qualquer é dada por:
vparafuso = v0 – g.t, t > t0
Em que g é a aceleração da gravidade, portanto para um observador dentro do elevador, a velocidade do parafuso será:
Vparafuso-elevador = Vparafuso – Velevador = v0 – g.t – v0 = – g.t, t > t0
Assim, no momento t0 o parafuso, em relação ao chão do elevador, inicia um movimento de queda livre a partir do repouso, ou seja, sua velocidade será linearmente proporcional ao tempo. Orientando o sentido da velocidade como positivo para baixo (Vparafuso-elevador = g.t) , o gráfico velocidade x tempo do parafuso deve ter o seguinte formato:
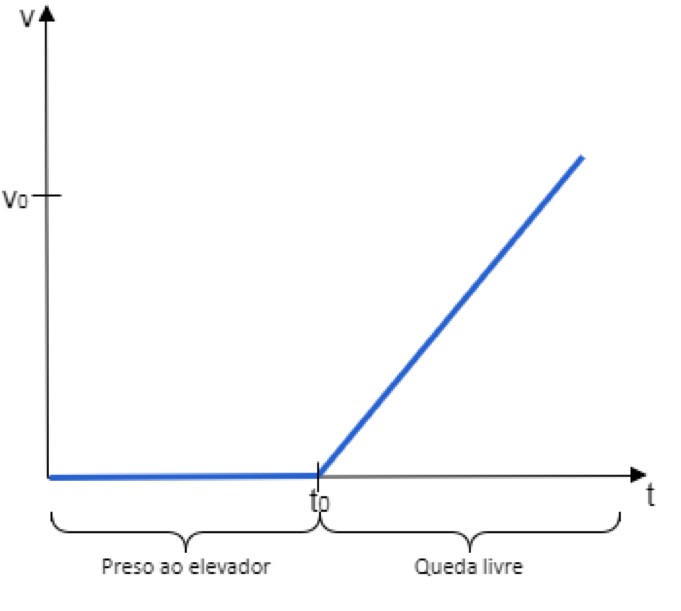
letra E
