Na estratosfera, há um ciclo constante de criação e destruição do ozônio. A equação que representa a destruição do ozônio pela ação da luz ultravioleta solar (UV) é
O gráfico representa a energia potencial de ligação entre um dos átomos de oxigênio que constitui a molécula de O3 e os outros dois como função da distância de separação r.
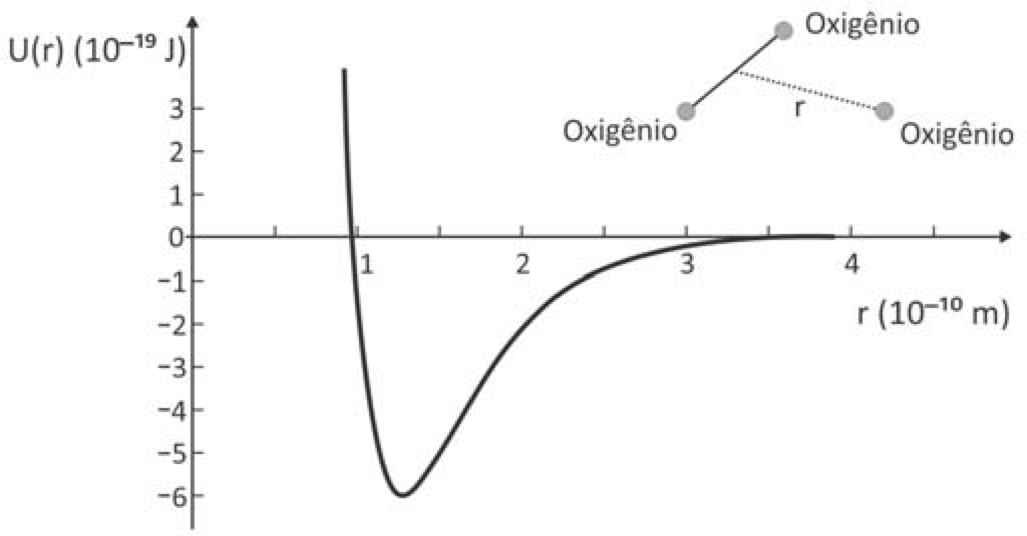
A frequência dos fótons da luz ultravioleta que corresponde à energia de quebra de uma ligação da molécula de ozônio para formar uma molécula de O2 e um átomo de oxigênio é, aproximadamente,
a) 1 x 1015 Hz
b) 2 x 1015 Hz
c) 3 x 1015 Hz
d) 4 x 1015 Hz
e) 5 x 1015 Hz
| Note e adote:
E = hf E é a energia do fóton. f é a frequência da luz. Constante de Planck, h = 6 x 10 34 J s |
Tags – Física, ligação covalente, energia de dissociação, energia potencial de ligação, poço de potencial, físico-química, energia do fóton, cálculo de frequência de fótons.
Resolução
Na visão clássica da ligação covalente, devido às diversas forças que surgem na aproximação de dois átomos (repulsão entre partículas de mesma carga e atração entre partículas de cargas opostas), todo par de átomos possui um comprimento de ligação ideal no qual a energia potencial entre esses é mínima e, portanto, a estabilidade é máxima.
No gráfico a baixo temos a curva de energia potencial (Ep) pela distância internuclear que mostra a variação da energia potencial entre os átomos em função da distância entre seus núcleos:
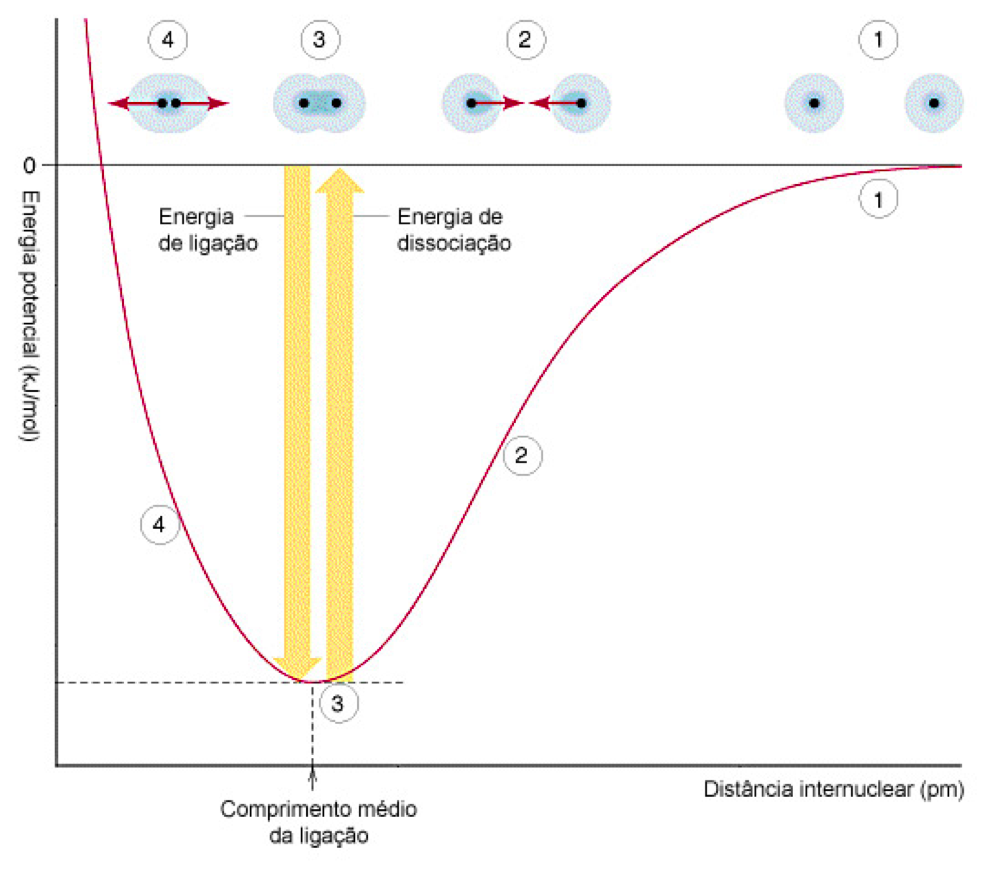
Na situação 1 os dois átomos estão muito afastados um do outro, praticamente não há atração entre eles e a energia potencial entre eles é quase nula; na situação 2 eles estão pouco afastados, propiciando a atração entre eles, o que torna a energia total dos dois átomos menor que a da situação 1 e, portanto, mais estável; na situação 3 temos o comprimento médio de ligação e neste ponto considera-se que a ligação covalente está formada. Há um equilíbrio entre as forças de atração e as forças de repulsão e a energia potencial da molécula é mínima; na situação 4 a repulsão entre os núcleos começa a ser maior que as atrações entre os elétrons e os núcleos, aumentando a instabilidade da molécula e a sua energia potencial.
A partir do ponto de energia mínima, se aproximarmos (situação 4) os átomos a repulsão entre os núcleos fará com que eles se afastem e voltem à posição de equilíbrio (situação 3), se afastarmos os átomos (situação 2) a atração entre elétrons e núcleos fará com que eles se aproximem e voltem à posição de equilíbrio até um ponto de distanciamento máximo (situação 1) no qual praticamente não exista mais interação eletrostática entre eles e dizemos que ouve a quebra da ligação.
No problema temos uma situação análoga no qual um dos átomos é substituído por uma molécula de O2 e a distância considerada é a distância do átomo isolado de oxigênio (O) ao centro de massa da molécula. Assim, a energia necessária para a quebra da ligação de ozônio será a diferença entre a energia do ponto da quebra e a energia do ponto de equilíbrio:

Eq = 0 J – (-6 x 10-19) J = 6 x 10-19 J
Portanto, um fóton precisa ter essa energia para que ele consiga romper uma ligação de uma molécula de ozônio. Substituindo o valor encontrado na fórmula dada pelo problema para a energia do fóton:
E = hf → 6 x 10-19 J = 6 x 10-34 J.s . f → f = 1 x 1015 Hz
letra A
