Em uma aula de laboratório de física, utilizando se o arranjo experimental esquematizado na figura, foi medido o índice de refração de um material sintético chamado poliestireno. Nessa experiência, radiação eletromagnética, proveniente de um gerador de micro ondas, propaga se no ar e incide perpendicularmente em um dos lados de um bloco de poliestireno, cuja seção reta é um triângulo retângulo, que tem um dos ângulos medindo 25o, conforme a figura. Um detetor de micro-ondas indica que a radiação eletromagnética sai do bloco propagando se no ar em uma direção que forma um ângulo de 15o com a de incidência.
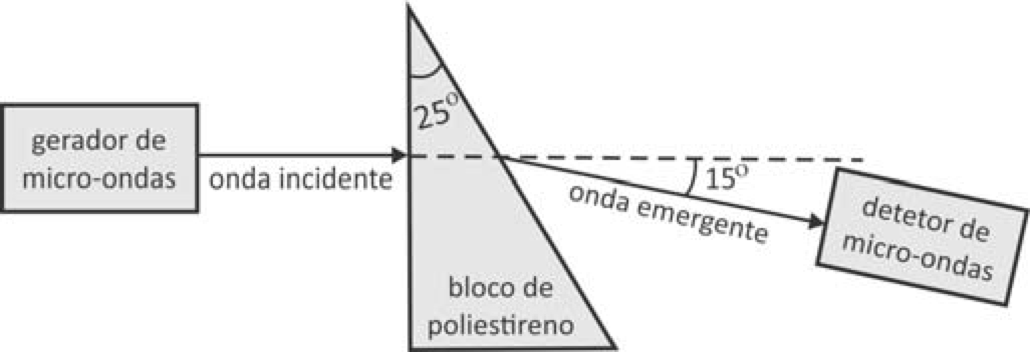
A partir desse resultado, conclui se que o índice de refração do poliestireno em relação ao ar para essa micro onda é, aproximadamente,
a) 1,3
b) 1,5
c) 1,7
d) 2,0
e) 2,2
| Note e adote:
Índice de refração do ar: 1,0 sen 15o ≈ 0,3 sen 25° ≈ 0,4 sen 40° ≈ 0,6 |
Tags – Física, óptica, refração, índice de refração, Lei de Snell, 2ª Lei da Refração, Lei de Snell-Descartes, ângulo de refração.
Resolução
Quando a luz passa de um meio para outro diferente sua frequência não é alterada, mas sua velocidade e o seu comprimento de onda são. Por essa mudança de velocidade ocorre um desvio em sua direção de propagação, que pode ser determinado usando a Lei de Snell (2ª Lei da Refração, Lei de Snell-Descartes).
Segunda Lei de Snell para um raio de luz monocromática passando de um meio para o outro, o produto do seno do ângulo, formado pelo raio e pela normal da interface em que ele incide, com o índice de refração em que se encontra esse raio é constante.
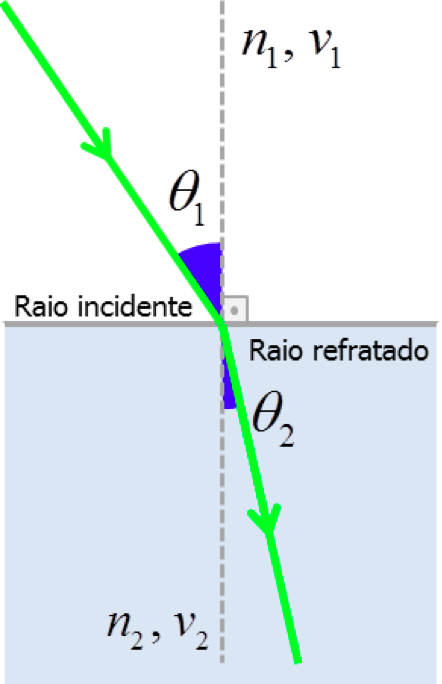
n1.senθ1 = n2.senθ2
De acordo com o enunciado temos a seguinte situação:
Portanto, o ângulo de incidência sobre a superfície inclinada do bloco de poliestireno e o de refração são, respectivamente, 25º e 40º e o índice de refração do ar fornecido pelo problema é 1, substituindo na equação da Lei de Snell:
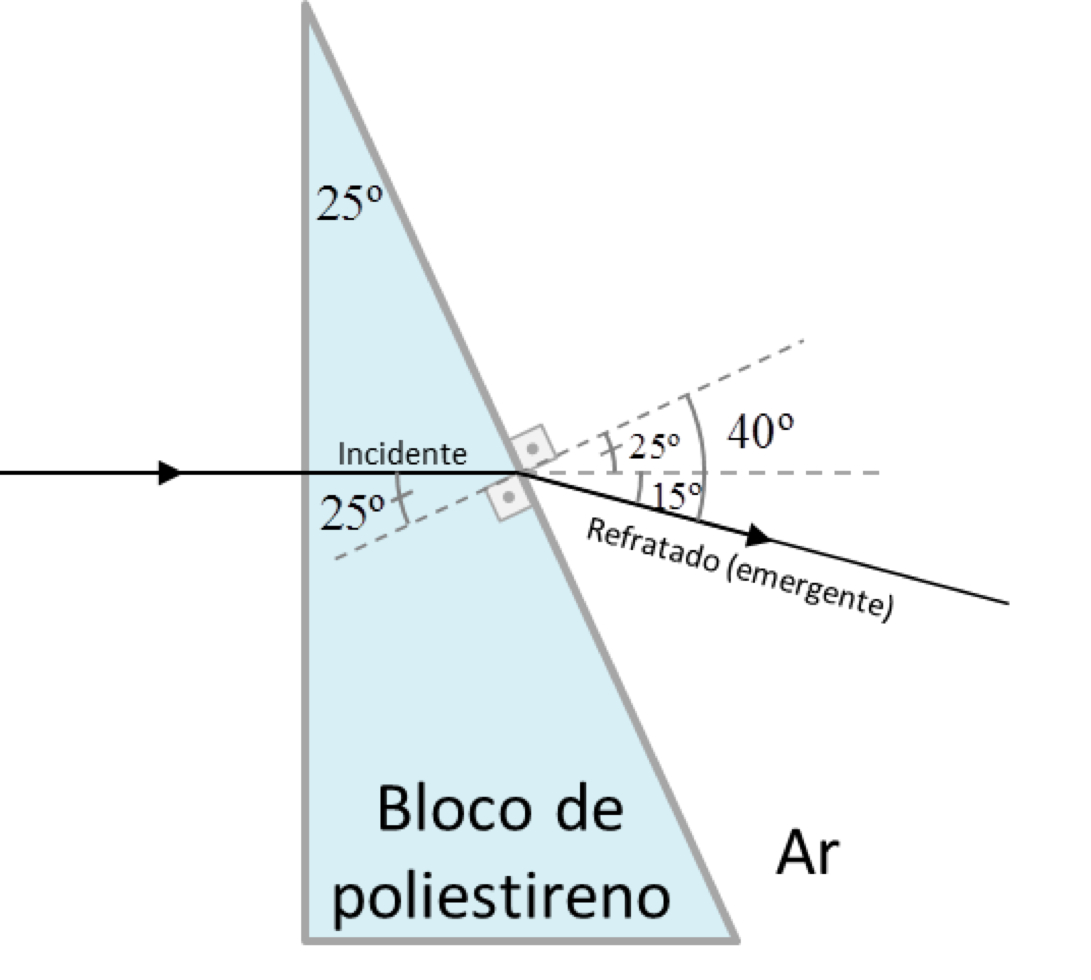
nbloco.sen(25º) = nAr.sen(40º)
→ nbloco = nAr.sen(40º)/sen(25º)
→ nbloco = 1.0,6/0,4 = 1,5
Alternativa B.
