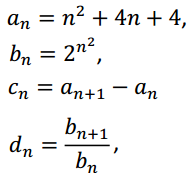Fuvest 2015. Prova V. Questão 52. PG e PA

52 Dadas as sequências

definidas para valores inteiros positivos de n, considere as seguintes afirmações:

I. an é uma progressão geométrica;

II. bn é uma progressão geométrica;

III. cn é uma progressão aritmética;

IV. dn é uma progressão geométrica.

São verdadeiras apenas

a) I, II e III.

b) I, II e IV.

c) I e III.

d) II e IV.

e) III e IV.

Resposta E

Uma progressão aritmética (P. A.) é uma sequência em que cada termo, a partir do segundo, é igual à soma do termo anterior com uma constante    é definido como razão da progressão aritmética. Assim, o termo n é igual ao termo (n-1) mais r:

a_n = a_n-1 + r

Fórmula geral de uma PA:

a_n = a₁ + (n-1)*r

Uma progressão geométrica é uma sequência numérica em que cada termo, a partir do segundo, é igual ao produto do termo anterior por uma constante, chamada de razão da PG. Fórmula geral:

a_n+1=a_n*q

Na questão temos:

I) an = n² + 4n + 4 ⇔ an = (n + 2)² não satisfaz a fórmula geral para PA nem para PG.

II) bn = 2ⁿ² não é PA nem PG

III) cn = an + 1 – an = (n + 3)² – (n + 2)² ⇔ cn = 2n + 5

⇒ (cn) = (7; 9; 11; …) é uma progressão aritmética de razão 2

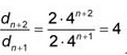
d) dn é uma progressão geométrica de razão 4.

 

Veja nosso resumo de PA.