A distribuição de salários pagos em uma empresa pode ser analisada destacando-se a parcela do total da massa salarial que é paga aos 10% que recebem os maiores salários. Isso pode ser representado na forma de um gráfico formado por dois segmentos de reta, unidos em um ponto P, cuja abscissa tem valor igual a 90, como ilustrado na figura.
No eixo horizontal do gráfico tem-se o percentual de funcionários, ordenados de forma crescente pelos valores de seus salários, e no eixo vertical tem-se o percentual do total da massa salarial de todos os funcionários.
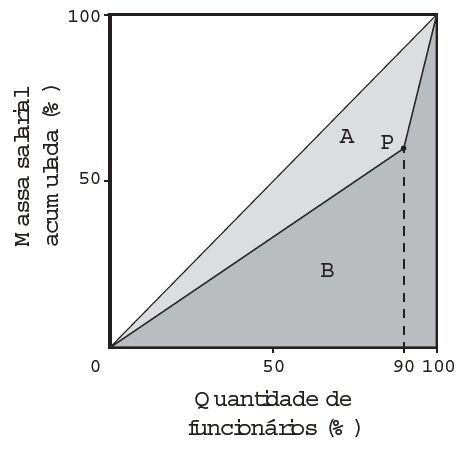
O índice de Gini, que mede o grau de concentração de renda de um determinado grupo, pode ser calculado pela razão A/(A+B), em que A e B são as medidas das áreas indicadas no gráfico.
A empresa tem como meta tornar seu índice de Gini igual ao do país, que é 0,3. Para tanto, precisa ajustar os salários de modo a alterar o percentual que representa a parcela recebida pelos 10% dos funcionários de maior salário em relação ao total da massa salarial.
Disponível em: www.ipea.gov.br. Acesso em: 4 maio 2016 (adaptado).
Para atingir a meta desejada, o percentual deve ser
- 40 %
- 20 %
- 60 %
- 30 %
- 70 %
SOLUÇÃO
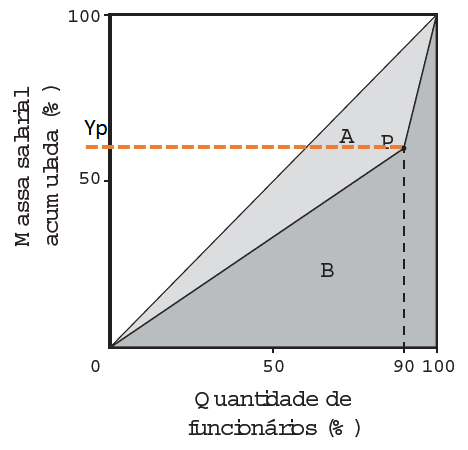
Yp será o ponto do ajuste percentual, podemos escrever:
Para área B:
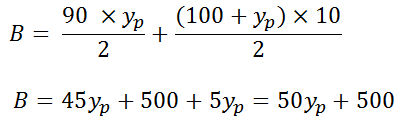
Para área A + B:
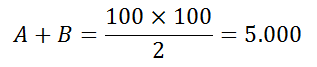
Para área A: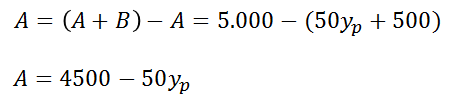
Aplicando a equação de Gini:
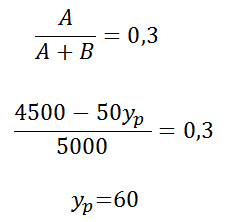
Esse yp = 60 nos mostra que 90% dos funcionários receberão 60% da soma total dos salários.
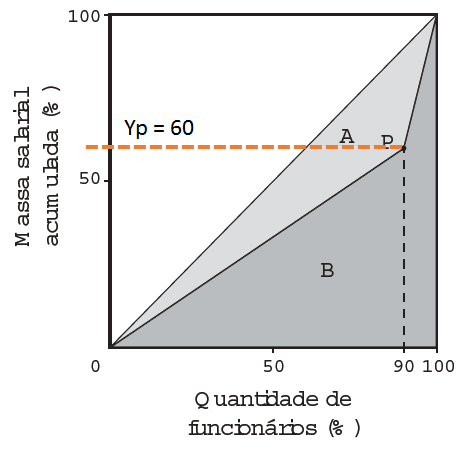
A questão nos pede o percentual recebido pelos 10% que ganham mais, que será justamente:
100 – 60 = 40 %.
Entendemos que essa questão não foi muito bem explicada, principalmente na rapidez com que a prova deve ser feita. De qualquer maneira, fica a solução.
LETRA A
