Para o modelo de um troféu foi escolhido um poliedro P, obtido a partir de cortes nos vértices de um cubo. Com um corte plano em cada um dos cantos do cubo, retira-se o canto, que é um tetraedro de arestas menores do que metade da aresta do cubo. Cada face do poliedro P, então, é pintada usando uma cor distinta das demais faces.
Com base nas informações, qual é a quantidade de cores que serão utilizadas na pintura das faces do troféu?
a) 6
b) 8
c) 14
d) 24
e)30
Solução
Vamos pegar um cubo.
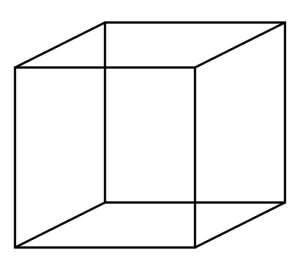
Em seguida, tiramos as “quinas” dele (encontro de 3 faces.):
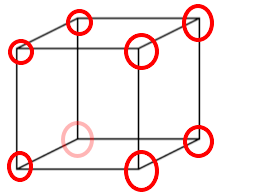
Cada uma dessas quinas vira uma face triangular. Como fizemos esse procedimento em oito “quinas”, teremos 8 faces triangulares a mais.
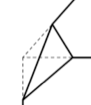
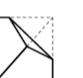
Quando retiramos todos os cantos do cubo, passamos a ter um sólido com 6 faces octogonais e 8 faces triangulares.
Logo, sabemos que cada face será pintada com uma cor diferente das demais, assim serão necessárias (6 + 8) cores = 14
cores.
Ou seja, aqui só precisamos saber quantas faces teremos, 6 faces do cubo mais 8 faces das “quinas” recém removidas do cubo.
Letra C.
