Uma lata de tinta, com a forma de um paralelepípedo retangular reto, tem as dimensões, em centímetros, mostradas na figura.
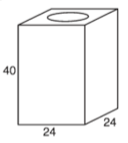
Será produzida uma nova lata, com os mesmos formato e volume, de tal modo que as dimensões de sua base sejam 25% maiores que as da lata atual. Para obter a altura da nova lata, a altura da lata atual deve ser reduzida em
a) 14,4%
b) 20,0%
c) 32,0%
d) 36,0%
e) 64,0%
Resposta
A questão nos fala que será produzida uma nova lata com mesmo formato (continuará sendo um paralelepípedo) e mesmo volume. Ele nos diz ainda que as dimensões da base serão aumentadas em 25%. Então se antes eram a, agora serão (1+0,25)a = 1,25 a
Lembremos que o volume de um paralelepípedo de é dado pela área da base vezes a altura:
V = Ab x H,
Vinicial = a*a*H
Vfinal = 1,25a*1,25a*hfinal
Igualando os volumes, temos:
a*a*H = 1,25a*1,25a*hfinal
Assim, temos:
H = 1,252hfinal
hfinal = H/1,252
Sabemos que 1,25 = 5/4, então:
hfinal = H/1,252 = H*(4/5)2 = H*16/25
Multiplicando por 4 em cima e embaixo (para evitar contas mais complicadas):
hfinal = H*16/25 *4/4= H*64/100=0,64H
Logo, hfinal = 0,64H = 64%H
Dessa forma, é precisa reduzir a altura H em H – 0,64H = 0,36H = 36%.
Letra D
