ENEM 2013 Numa escola com 1 200 alunos foi realizada uma pesquisa sobre o conhecimento desses

Numa escola com 1 200 alunos foi realizada uma pesquisa sobre o conhecimento desses em duas línguas estrangeiras, inglês e espanhol.

Nessa pesquisa constatou-se que 600 alunos falam inglês, 500 falam espanhol e 300 não falam qualquer um desses idiomas.

1. 1/2
2. 5/8
3. 1/4
4. 5/6
5. 5/14

SOLUÇÃO

Precisamos fazer o diagrama de Venn:

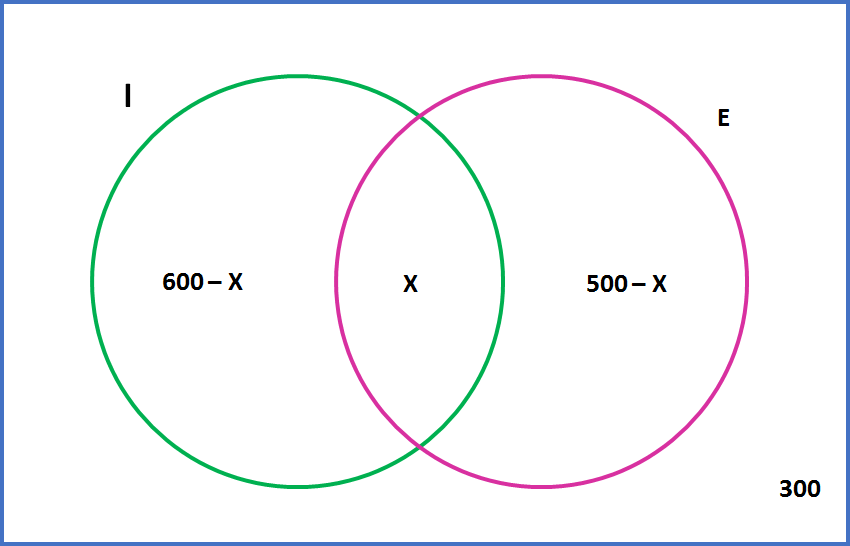
Como o total de alunos entrevistados é 1200, temos que a soma será:

(600 – x) + x + (500 – x) + 300 = 1200

x = 200

Assim, ficamos com:

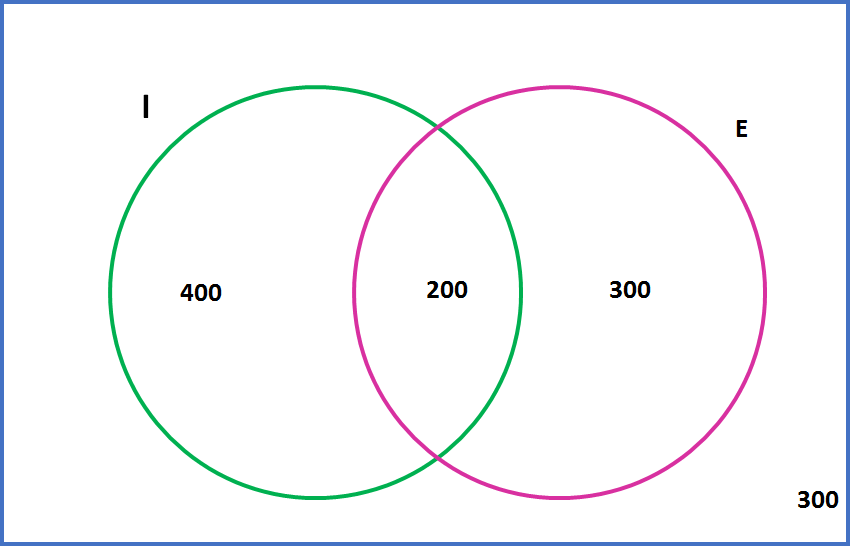
Como o número de alunos que fala inglês é 600, o total que não fala inglês será o complementar de I:

I^C = 1200 – 600 = 600

Entre esses alunos, aqueles que falam espanhol será a parte amarela da figura:

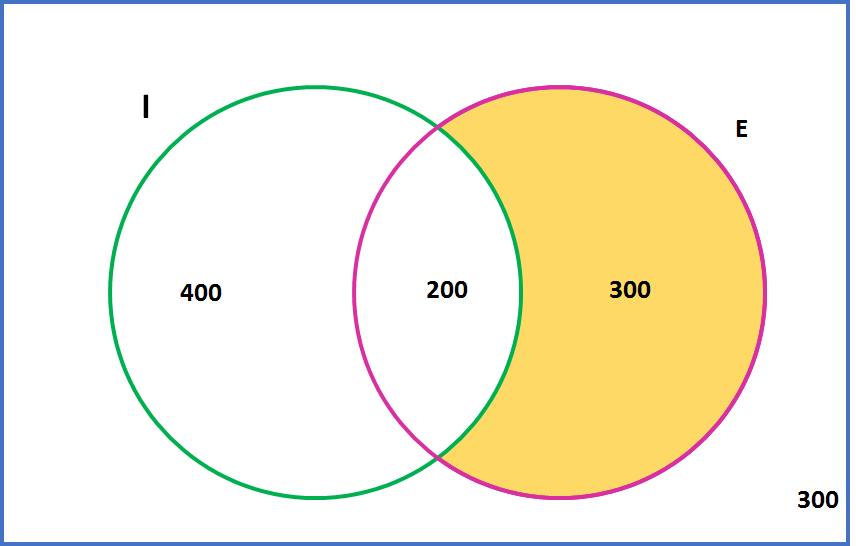
I^C ∩ E = 500 – x = 500 – 200 = 300

Logo, a probabilidade pedida será:

P = (I^C ∩ E)/I^C = 300 / 600 = 1/2

LETRA A