Furacões são sistemas físicos que liberam uma enorme quantidade de energia por meio de diferentes tipos de processos, sendo um deles a condensação do vapor em água. De acordo com o Laboratório Oceanográfico e Meteorológico do Atlântico, um furacão produz, em média, 1,5 cm de chuva por dia em uma região plana de 660 km de raio. Nesse caso, a quantidade de energia por unidade de tempo envolvida no processo de condensação do vapor em água da chuva é, aproximadamente,
(A) 3,8 1015 W.
(B) 4,6 1014 W.
(C) 2,1 1013 W.
(D) 1,2 1012 W.
(E) 1,1 1011 W.
| Note e adote: π = 3.
Calor latente de vaporização da água: 2 x 106 J/kg. Densidade da água: 103 kg/m3. 1 dia = 8,6 x 104 s. |
Tags – Física, Potência, Calor Latente, Índice Pluviométrico, mudança de fase da água.
Resolução
O problema nos pede a quantidade de energia por unidade de tempo – potência(P) – para evaporar a água da chuva de um dia. O tempo nos é dado (1 dia = 8,6 x 104s), portanto, nos resta determinarmos a energia necessária para evaporarmos a massa de chuva de um dia.
Desconsiderando o processo de aquecimento da água, calculando apenas o calor necessário para passar a água líquida em sua temperatura de ebulição para o estado de vapor na mesma temperatura, temos que a energia empregada nessa transformação é dada por:
Qlatente = m x L
Em que L é o calor latente de vaporização da água fornecido pelo problema e m a massa de chuva que devemos calcular.
O índice pluviométrico refere-se à quantidade de chuva por metro quadrado em determinado local e é medido através do uso de pluviômetros.

Isso significa que se dizermos que choveu 1,5 cm por dia em uma região, equivale a se tivéssemos nesse local uma caixa aberta, com 1 metro quadrado de base, e o nível da água dentro dela atingisse 1,5 cm de altura. Portanto na região plana de 660 km de raio choveu o volume equivalente a um cilindro de base 660 km e altura 1,5 cm:
Vchuva = 1,5 x 10-2 x π x (660 x 103)2 ≈ 19,6 x 109m3
O problema também nos fornece a densidade da água, portanto podemos calcular a massa de chuva através dela. Sabemos da definição de densidade que:
densidade = massa / volume
massa = densidade x volume
Substituindo na equação acima o valor da densidade e do volume:’
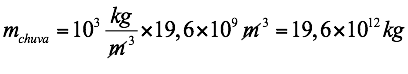
Voltando à equação da quantidade de calor latente:
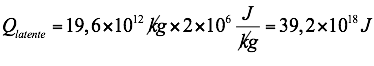
Dividindo pelo tempo, chegamos à alternativa B:
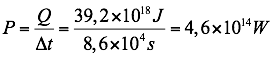
letra D
