Um engenheiro projetou um automóvel cujos vidros das portas dianteiras foram desenhados de forma que suas bordas superiores fossem representadas pela curva de equação y = log(x), conforme a figura.
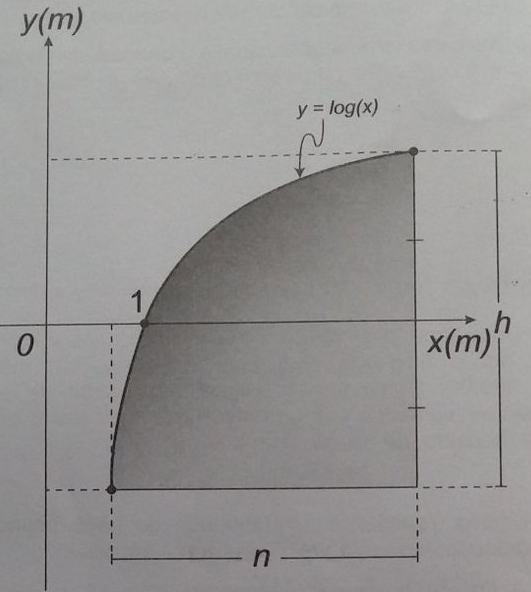
A forma do vidro foi concebida de modo que o eixo x sempre divida ao meio a altura h do vidro e a bsas do vidro seja paralela ao eixo x. Obedecendo a essas condições, o engenheiro determineou uma expressão que fornece a altura h do vidro em função da medida n de sua base, em metros.
A expressão algébrica que determina a altura do vidro é
a)
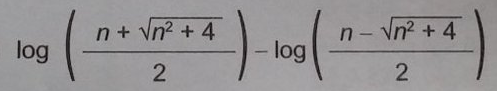
b)
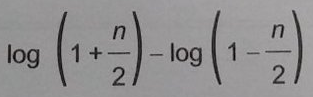
c)
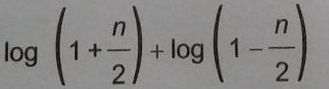
d)
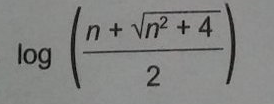
e)
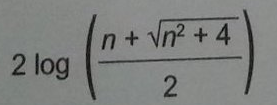
Resolução
Primeiro vamos relembrar as propriedades dos logaritmos:
Agora, tomemos os pontos do gráfico que vão nos ajudar a resolver a questão. Queremos ter uma relação entre h e n (como a questão pede). Para isso, vamos estabelecer um ponto de abscissa x (rosa), no gráfico, e um ponto de abscissa x+n (verde).
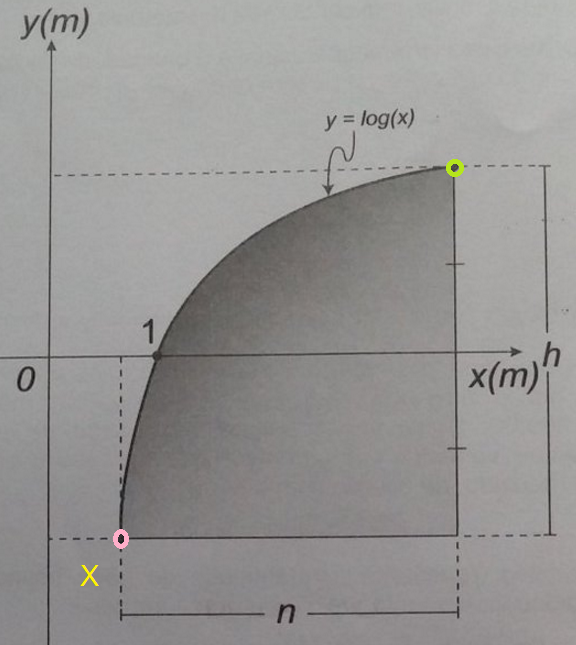
Agora juntando a abscissa e a ordenada, temos os pontos:
ponto rosa: (x, -h/2)
ponto verde: (x+n, h/2).
(para os daltônicos, rosa está na esquerda inferior e verde na direita superior)
Como os pontos estão na curva y = log(x), podemos aplicar a equação para encontrar as equações:
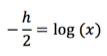(eq. 1)
(eq. 2)
Somando as equações 1 e 2, temos:
logx + log (x+n) = 0
Propriedades da soma de log:
logx + log (x+n) = log[x.(x+n)]=0
Logo, x.(x+n) = 100=1
x2+nx-1=0
Resolvendo por Báskara:
O valor negativo de x não existe pela nossa hipótese
Logo,
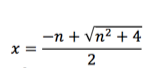
Usando a eq. 2:
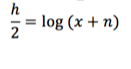
Substituindo o x:
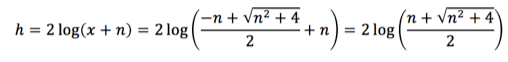
Letra E
